Urti anelastici

Negli urti anelastici l’energia cinetica del sistema non si conserva.
Il più delle volte diminuisce, ma ci sono anche casi in cui può aumentare come, ad esempio, quando l’urto produce un’esplosione.
Consideriamo l’urto anelastico di due corpi di masse \(m_1\) e \(m_2\) che si muovono prima dell’urto con velocità \(\vec{v}_{1,i}\) e \(\vec{v}_{2,i}\). Se chiamiamo \(\vec{v}_{1,f}\) e \(\vec{v}_{2,f}\) le velocità dei due corpi dopo l’urto, allora la conservazione della quantità di moto totale del sistema si scrive come:

Osserviamo che, pur conoscendo le masse e le velocità iniziali dei corpi, non siamo in grado di ricavare le velocità finali dopo l’urto da quest’unica relazione. Infatti, da un punto di vista matematico, abbiamo una sola equazione nella quale compaiono due incognite e abbiamo, pertanto, bisogno di un’ulteriore informazione.
Esiste, tuttavia, un particolare caso di urto anelastico per il quale la sola conservazione della quantità di moto totale del sistema è sufficiente per determinare la velocità finale dei corpi: l’urto completamente anelastico.
In un urto completamente anelastico i due corpi, inizialmente separati, rimangono uniti dopo l’urto in un unico corpo, muovendosi, quindi, con la stessa velocità.
Seppure, come per gli urti elastici, nella realtà non esistono urti completamente anelastici, in buona approssimazione sono esempi di questo tipo di urto un proiettile che entra in un sacco pieno di sabbia o due vagoni che entrando a contatto si agganciano tramite un magnete.

In questo caso possiamo semplificare la notazione chiamando \(\vec{v_{1}}\) e \(\vec{v_{2}}\) le velocità iniziali dei corpi e \(\vec{v_{f}}\) la loro velocità finale, dopo l’urto. La conservazione della quantità di moto totale del sistema diventa, allora:

Da questa relazione è possibile ricavare direttamente la velocità finale dei corpi dopo l’urto:

Per capire più a fondo il significato della relazione, supponiamo che l’urto avvenga lungo una retta. Avremo, quindi:

dove \({v_{1}}\), \({v_{2}}\) e \({v_{f}}\) sono i moduli delle velocità scritte con segno positivo se il moto è nel verso positivo del sistema di riferimento e con segno negativo nel caso contrario. Dunque, la velocità finale del sistema è la media ponderata delle velocità iniziali dei due corpi, con le masse che assumono il ruolo di pesi.
In particolare se i due corpi hanno la stessa massa \({m}\), la velocità finale assume valore:

Perciò, in questo caso, la velocità finale è proprio la media aritmetica delle velocità iniziali dei due corpi.
Di particolare interesse sono, poi, i casi in cui uno dei due corpi è fermo e l’altro lo colpisce.
Supponiamo che il corpo fermo sia quello di massa \(m_2\), esso prenderà il nome di bersaglio, mentre il corpo di massa \(m_1\) prende il nome di proiettile. Poiché \( v_{2}=0 \), la velocità finale sarà data dalla relazione:

Distinguiamo tre casi a seconda della relazione che intercorre tra la massa del proiettile e quella del bersaglio.
1) La massa del proiettile è molto maggiore della massa del bersaglio \(m_1\) >> \(m_2\) , quindi:

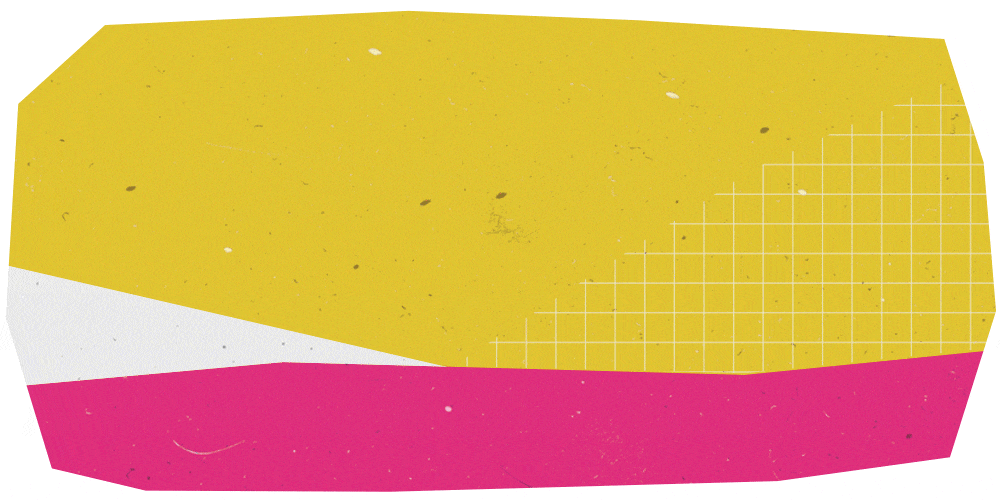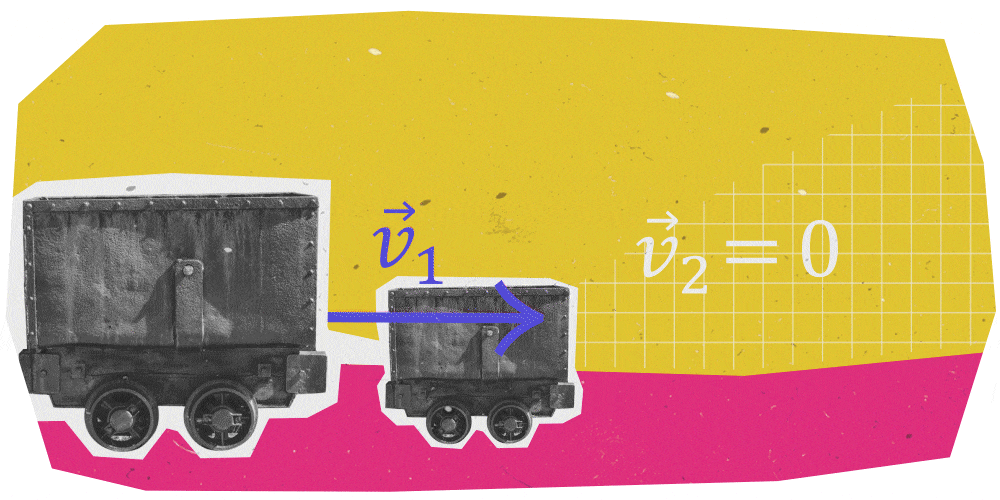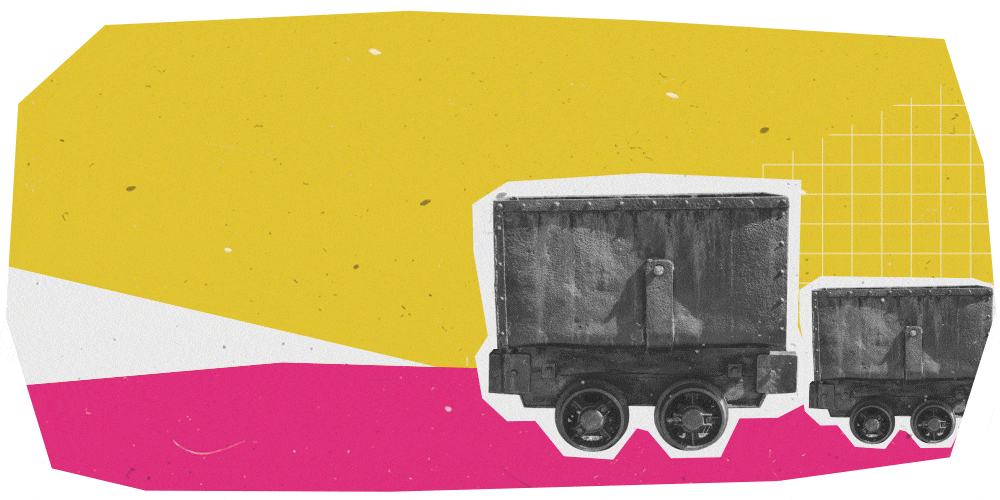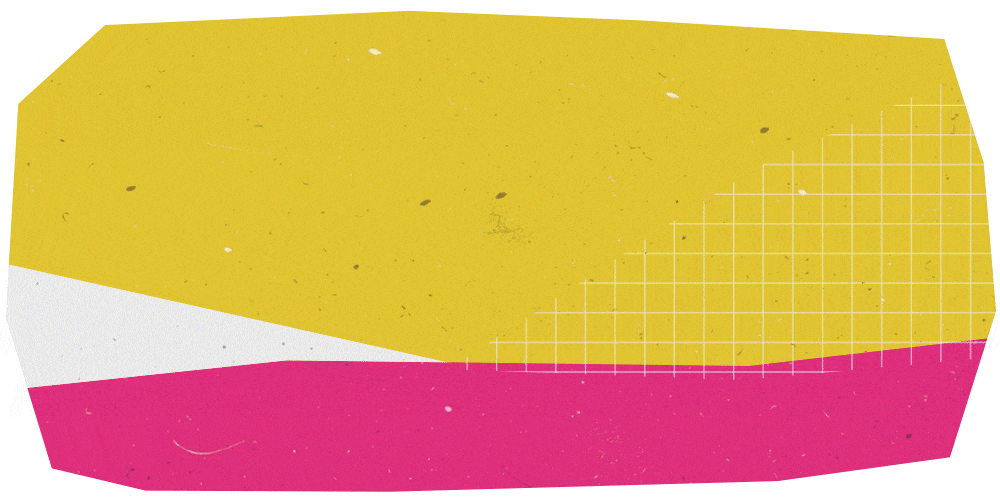
In questo caso la velocità finale è pressoché uguale a quella del proiettile, come se il bersaglio, in virtù della sua piccola massa, non influisse sul moto del proiettile che continua, invece, dritto sulla sua traiettoria. È quello che succede, ad esempio, quando un moscerino, fermo a mezz’aria, si schianta sul parabrezza di un’auto.
2) La massa del proiettile è uguale alla massa del bersaglio \(m_1\) = \(m_2\) , quindi:


In questo caso la velocità finale è la metà della velocità del proiettile.
Il bersaglio rallenta il proiettile in misura pari al rapporto tra la sua massa e la massa totale del sistema.
3) La massa del proiettile è molto minore della massa del bersaglio \(m_1\) << \(m_2\), quindi:


In questo caso la velocità finale è pressoché nulla, come se il bersaglio, in virtù della sua grande massa, bloccasse totalmente il moto del proiettile. È quello che succede, ad esempio, quando una freccetta si conficca all’interno di un bersaglio appeso a un muro.
Abbiamo supposto che l’urto completamente anelastico avvenisse lungo una retta per capirne meglio alcuni aspetti.
Tuttavia, molti degli urti completamente anelastici che avvengono nel quotidiano sono urti bidimensionali: un placcaggio nel rugby o un incidente stradale a un incrocio, ad esempio. D’altra parte avevamo ricavato un’espressione per la velocità finale in forma vettoriale e, quindi, valida anche per urti completamente anelastici che avvengono su un piano. In questo caso per operare praticamente con l’espressione:

è necessario scomporla nelle componenti \(x\) e \(y\) del sistema di riferimento:


Stiamo così implicitamente sfruttando la conservazione della quantità di moto totale del sistema su tutte le componenti del sistema di riferimento.