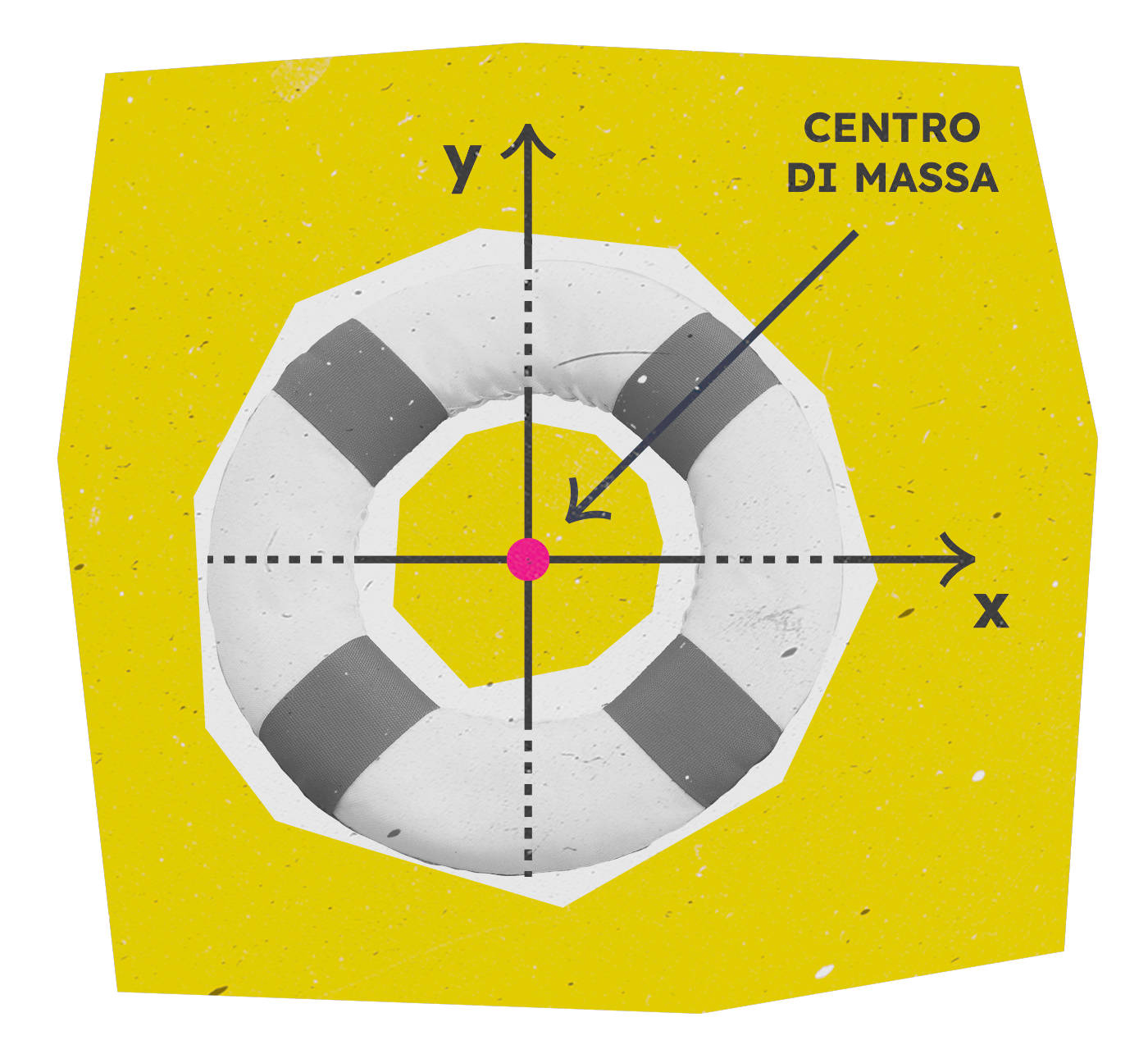
Il centro di massa

Sebbene la conservazione della quantità di moto ci consenta di studiare diversi sistemi, ci sono però dei casi che risultano ancora difficili da trattare, come quello di un fuoco d’artificio che vola in alto e poi esplode o di un boomerang che viene lanciato e torna indietro.
In queste situazioni, la sola conservazione della quantità di moto non è sufficiente a descrivere la traiettoria di tutti i frammenti del fuoco d’artificio o di tutti i punti del boomerang. Per questo motivo introduciamo un nuovo concetto: il centro di massa di un sistema di corpi.
Prima di andare a darne la definizione formale, cerchiamo di provare a individuarlo in un sistema di corpi molto semplice, come può essere il bilanciere del sollevamento pesi. Date le dimensioni ridotte del sistema, possiamo assumere che il centro di massa coincida con il baricentro, cioè il punto in cui si considera concentrata la forza peso agente sul sistema. Quindi, se si appende il bilanciere a un filo passante per il centro di massa, esso sarà in equilibrio orizzontalmente perché la tensione del filo bilancerà la forza peso del sistema.
Supponiamo inizialmente che sulle due estremità del bilanciere si trovino due pesi di egual massa.
Affinché esso sia in equilibrio, dovremo appenderlo esattamente al centro.

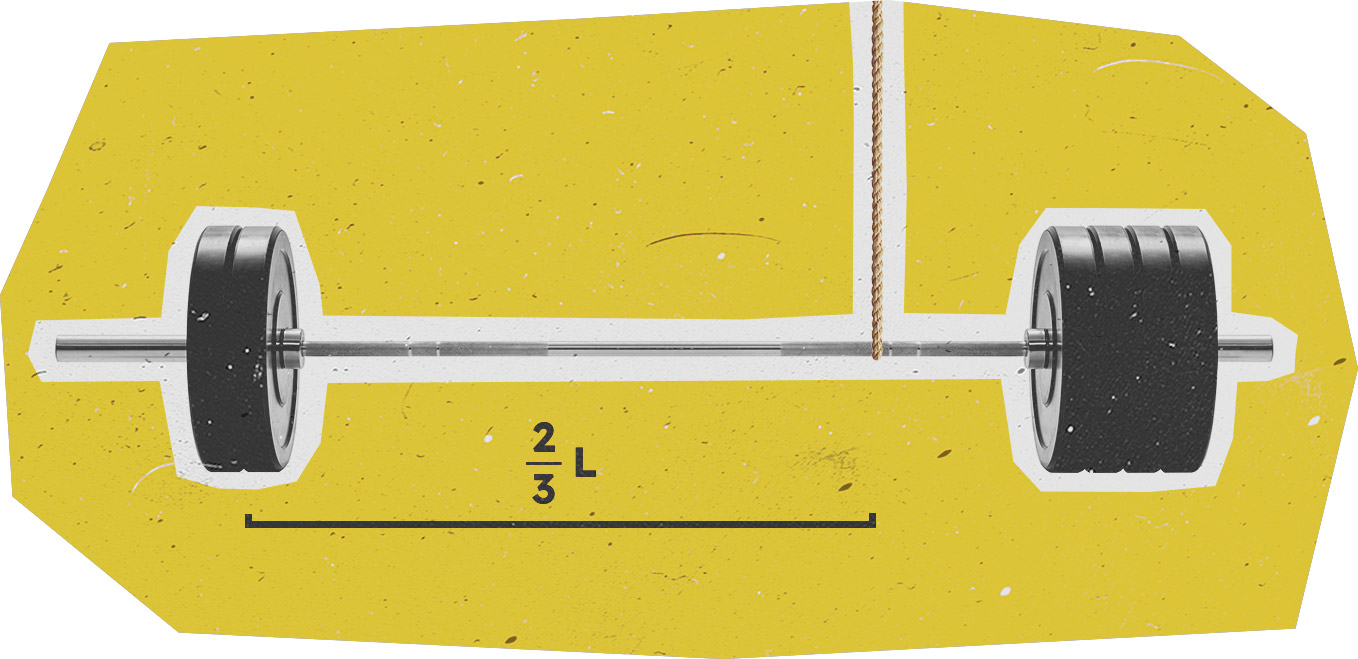
Se sull’estremità di sinistra dimezziamo la massa, allora, per avere equilibrio, dovremo spostare il punto a cui è appeso il filo verso destra.

Se scarichiamo completamente il bilanciere a sinistra, allora rimarranno solo i pesi di destra e sarà necessario appendere il filo in prossimità di questi ultimi al fine di tenere il bilanciere in posizione orizzontale.

L'esempio ci mostra come il centro di massa si comporti come la media ponderata delle posizioni dei corpi che compongono il sistema, in cui il ruolo dei pesi è assunto dalle masse dei corpi stessi. Perciò è proprio in questa maniera che definiamo la posizione del centro di massa \(x_{C M}\) per un sistema costituito da due corpi di massa \(m_{1}\) e \(m_{2}\) e posizione \(x_{1}\) e \(x_{2}\) :

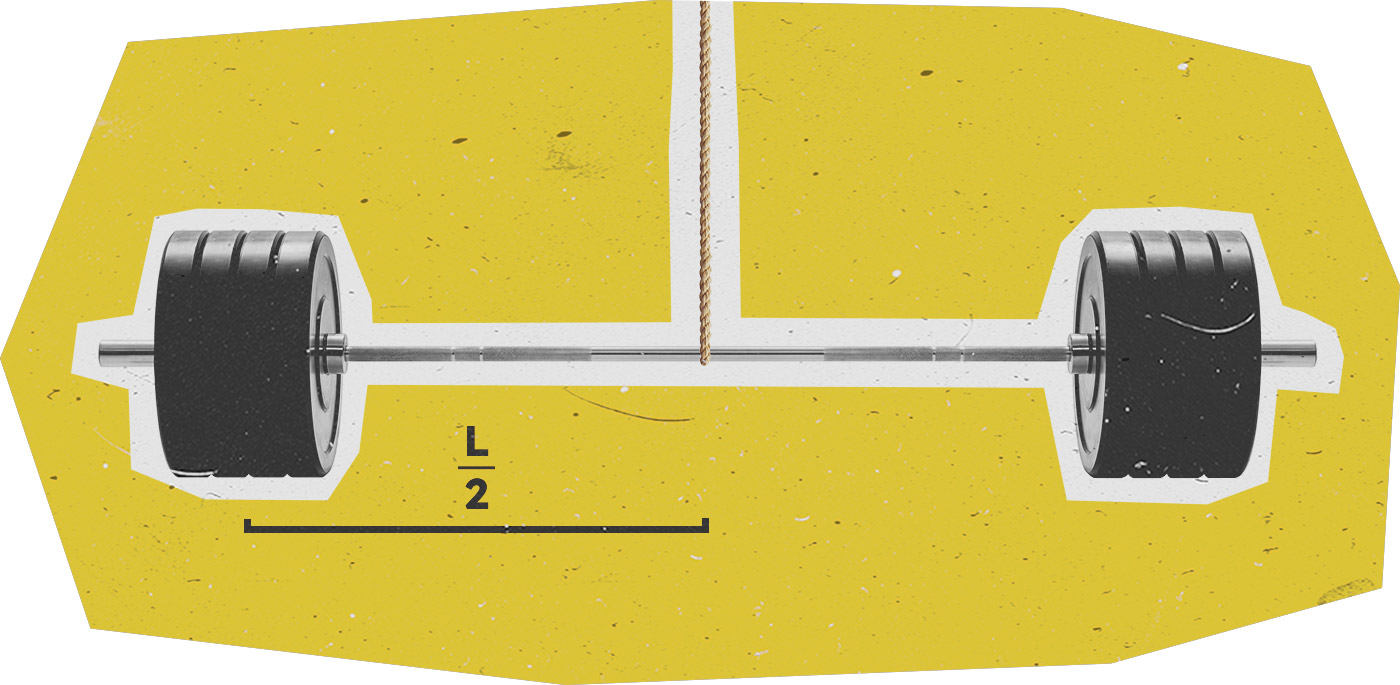

Osserviamo che la definizione è in accordo con le osservazioni sperimentali viste per il bilanciere. Infatti, se esso ha lunghezza \(L\) e si pone l'origine del sistema di riferimento nell'estremo di sinistra, all'inizio avremo che le masse hanno lo stesso valore \(m\), quindi:

Perciò il centro di massa è al centro del bilanciere. Se dimezziamo \(m_{1}\) otteniamo:

Quindi il centro di massa si sposta verso i due terzi del bilanciere. Infine quando \(m_{1}\) è nulla:

Dunque, il centro di massa coincide con la posizione dell’unica massa presente.
La definizione data per un sistema di due corpi può essere generalizzata a un sistema composto da un numero qualsiasi di corpi ed è valida per tutte e tre le componenti \(x\), \(y\) e \(z\) del sistema di riferimento:
Dato un sistema di \(n\) corpi di masse \(m_{1}, \ldots, m_{n}\) e posizioni \(\vec{r}_{1}=\left(x_{1}, y_{1}, z_{1}\right), \ldots, \vec{r}_{n}=\left(x_{n}, y_{n} \cdot z_{n}\right)\), le coordinate del centro di massa del sistema sono le medie ponderate delle coordinate dei corpi che compongono il sistema, in cui il ruolo dei pesi è assunto dalle masse dei corpi stessi:

Cioè, in coordinate:

Quando il sistema è non molto esteso, su tutti i corpi l’accelerazione di gravità assume lo stesso valore.
Sotto questa condizione, il centro di massa coincide con il baricentro del sistema. Questa condizione è sempre verificata dai corpi estesi a patto di considerarli come sistemi formati dai volumi che li compongono visti come punti materiali.
Ne segue che nel caso dei corpi estesi che presentano simmetrie, il centro di massa coincide con il centro di simmetria del corpo.