Conservazione della quantità di moto

Dalla legge fondamentale della dinamica in termini di quantità di moto sappiamo che:

Perciò, se la risultante delle forze che agiscono su un corpo nell'intervallo di tempo \(\Delta t=t_{f}-t_{i}\) è nulla, ne segue che:

Abbiamo così dimostrato il principio di conservazione della quantità di moto per un corpo:
Se la risultante delle forze agenti su un corpo è nulla, la quantità di moto del corpo si conserva:

Il risultato non stupisce dal momento che, se la risultante delle forze agenti su un corpo è nulla, esso non è sottoposto ad alcuna accelerazione, quindi la sua velocità resta costante.
Dal momento che resta costante anche la sua massa, ne segue che rimane costante anche la sua quantità di moto.
Può essere, allora, più utile generalizzare il risultato alla quantità di moto totale \(\vec{p}_{tot }\) di un sistema composto da più corpi: sotto quali condizioni avremo conservazione della quantità di moto totale?
Dovremo supporre che su ciascun corpo che compone il sistema la risultante delle forze agenti sia nulla?
L'esempio che segue mostra come in realtà sia sufficiente una richiesta meno restrittiva.
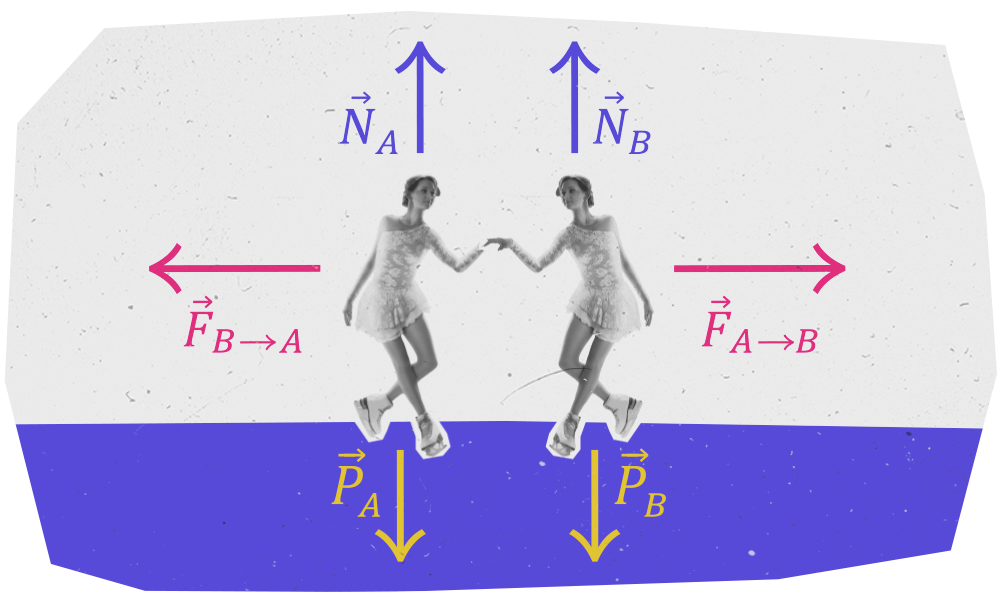
Consideriamo due pattinatrici su ghiaccio inizialmente ferme una di fronte all'altra e con le mani a contatto.
A un certo punto le due pattinatrici si danno una spinta e iniziano a muoversi in versi opposti.

Si può verificare sperimentalmente che, se le due pattinatrici hanno la stessa massa \(m\), allora anche le loro velocità hanno lo stesso modulo \(v\). Perciò:

D'altra parte, la quantità di moto totale iniziale del sistema \(p_{{tot}{,i}}\) era nulla perché le pattinatrici erano ferme, quindi essa si è conservata durante il moto.
Potremmo pensare che il risultato dipenda dal fatto che le due pattinatrici abbiano la stessa massa, ma, sostituendo la pattinatrice \(B\) con una bambina che ha massa \(m_{B}\) pari alla metà della massa della pattinatrice \(A\), possiamo verificare che la velocità della bambina ha modulo pari al doppio della velocità della pattinatrice adulta e, quindi, risulta ancora:

Perciò la quantità di moto totale del sistema si conserva in ogni caso, indipendentemente dalle masse delle due pattinatrici, nonostante su ciascuna di esse agisca una forza risultante non nulla. Ciò è dovuto al fatto che il sistema che stiamo considerando è un sistema isolato: per ciascuna pattinatrice, la forza peso e la reazione vincolare si bilanciano e quindi \(\vec{F}_{{est }}=0\) .
Questo risultato è tutto generale. Infatti, se scriviamo la legge fondamentale della dinamica in termini di quantità di moto per l’intero sistema, otteniamo:

Con \(\vec{F}_{{tot }}\) abbiamo indicato la risultante di tutte le forze che agiscono sul sistema, ma sappiamo che esse si dividono in forze interne e forze esterne, quindi:

Abbiamo già dimostrato che per qualsiasi sistema \(\vec{F}_{int }=0\). Pertanto:

Se assumiamo che il sistema sia isolato, avremo che anche \(\vec{F}_{{est }}=0\). Ne seguirà, dunque:

Abbiamo così dimostrato il principio di conservazione della quantità per sistemi isolati:
In un sistema isolato la quantità di moto totale del sistema si conserva:

È bene sottolineare come la conservazione della quantità di moto totale del sistema non implichi la conservazione della quantità di moto dei singoli corpi che lo compongono. Nell'esempio delle pattinatrici, la quantità di moto iniziale è, in un primo momento, nulla, sia per \(A\), sia per \(B\), ma dopo che si sono vicendevolmente spinte è diversa da zero per entrambe.
Questo significa che le forze interne possono modificare l’energia cinetica del sistema e, quindi, in generale, compiono lavoro.
La natura vettoriale del principio di conservazione della quantità di moto ci consente di applicarlo su ciascuna delle tre componenti \(x, y\) e \(z\) del nostro sistema di riferimento.
Ad esempio, supponiamo di aver spinto un carrello lungo la corsia di un supermercato e che si stia muovendo con velocità costante.
Tiriamo giù una scatola di biscotti da uno scaffale affinché cada perpendicolarmente nel carrello.
II sistema descritto non è isolato perché sulla scatola di biscotti agisce la forza peso, che non è una forza interna al sistema.
Tuttavia, essa è diretta lungo l'asse \(y\) quindi, non agiscono forze esterne nella direzione del moto, cioè lungo l’asse \(x\) .
Ne segue che lungo l'asse \(x\) la quantità di moto totale del sistema si conserva, cioè che \(\Delta p_{t o t, x}=0\) .

Applicare correttamente il principio di conservazione della quantità di moto non è utile soltanto a studiare sistemi di cui comprendiamo la dinamica, ma anche a dare una spiegazione a fenomeni più complessi come il rinculo di un'arma da fuoco o come la propulsione a reazione. Ti sarà sicuramente capitato di vedere nei film di azione che, quando un'arma da fuoco spara, tende a muoversi nel verso opposto rispetto al proiettile. Questo fenomeno prende il nome di rinculo ed è dovuto al fatto che l'arma da fuoco e il proiettile costituiscono un sistema isolato. All'inizio la quantità di moto totale del sistema è nulla. Con lo sparo, il proiettile di massa \(m\) acquista una velocità molto grande di modulo \(v\) e, di conseguenza, l'arma di massa \(M\) deve acquisire una velocità di rinculo di modulo \(V\) che abbia verso opposto rispetto a quella del proiettile:

Possiamo calcolare la velocità di rinculo, isolando \(V\) :

Poiché il rapporto tra la massa del proiettile \(m\) e quella dell'arma \(M\) è molto piccolo, la velocità di rinculo è molto minore rispetto alla velocità di partenza del proiettile.

Tuttavia, più il calibro del proiettile è grande e più il rapporto tra \(m\) e \(M\) tende ad aumentare e, quindi, tende ad essere maggiore la velocità di rinculo. Questo spiega perché, ad esempio, un fucile abbia un rinculo maggiore rispetto a una pistola.
Se il rinculo è un effetto indesiderato della conservazione della quantità di moto, la propulsione a reazione è, invece, una sua utile applicazione, che è alla base del moto di diversi dispositivi, primi tra tutti, i razzi. Quando un razzo si stacca da terra, espelle velocemente verso il basso una gran quantità di gas di scarico dovuta alla combustione di ossigeno e comburente contenuti nei suoi serbatoi interni.
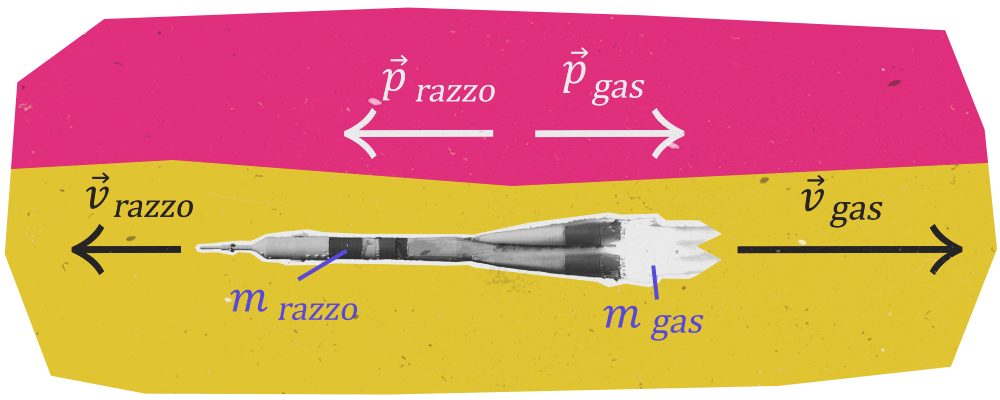
Contrariamente a quanto si possa pensare, però, non è né la presenza di un motore interno, né la spinta del gas verso il terreno che fanno acquisire al razzo velocità verso l’alto, bensì la conservazione della quantità di moto del sistema costituito dal razzo e dal gas applicata esattamente alla stessa maniera del rinculo.