Teorema dell’impulso

Prima abbiamo visto come sia la variazione di quantità di moto di un corpo \( \Delta{\vec{p}} \), sia l'impulso di una forza \(\vec{I}\) hanno la stessa unità di misura. Questo ci fa intuire che deve esistere una relazione tra queste due grandezze fisiche. Infatti, se riscriviamo la legge fondamentale della dinamica in termini di quantità di moto facendo riferimento alla forza media esercitata su un corpo, cioè:

e la combiniamo con la definizione di impulso di una forza \(\vec{F}\), otteniamo:

Questo risultato prende il nome di teorema dell’impulso:
L'impulso di una forza \(\vec{F}\) che agisce su un corpo per un intervallo di tempo \(\Delta t\) è uguale alla variazione di quantità di moto del corpo \(\Delta \vec{p}\) :

Pertanto, conoscendo le variazioni di quantità di moto di un corpo, possiamo stabilire qual è la forza media che ha agito su di esso.
Ad esempio, durante la battuta di una pallavolista, la palla parte da ferma e la sua velocità, subito dopo la battuta, viene registrata da una fotocellula presente sul campo. Conoscendo la massa della palla e stimando il tempo che la palla è a contatto con la mano del battitore, si può stabilire qual è la forza media che quest’ultimo ha impresso sulla palla.
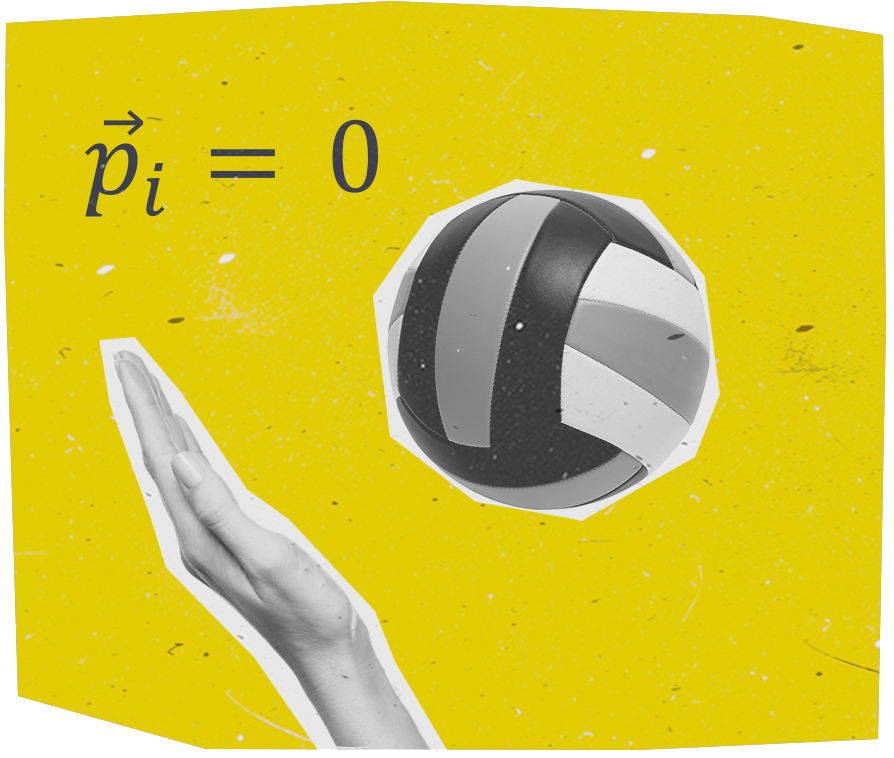


II teorema dell'impulso ci dice anche che, fissata la variazione di quantità di moto, il modulo della forza media \(F_{m}\) e l'intervallo di tempo nel quale agisce \(\Delta t\) sono inversamente proporzionali.
Questo spiega perché nel salto in alto o nel salto con l'asta si usino i materassini per attutire la caduta: il materassino, a contatto con l'atleta in caduta, si deforma e allunga, di conseguenza, il tempo di contatto \(\Delta t\) tra atleta e materasso.
Ne segue che deve diminuire la forza esercitata dal materasso sull'atleta e, questo, evita il rischio di possibili danni.
Lo stesso principio è alla base degli airbag delle automobili o, più semplicemente, spiega perché quando atterriamo al suolo tendiamo a piegare le ginocchia anziché tenerle tese.
