Forze impulsive e impulso di una forza

La legge fondamentale della dinamica è valida per ogni tipologia di forze, anche se nel dimostrarla, applicando il secondo principio della dinamica, abbiamo supposto che la forza risultante fosse costante.
Sebbene siamo soliti considerare le forze costanti, nel quotidiano ci sono molti esempi di forze che non sono costanti nel tempo: quella applicata da un martello su un chiodo, quella di una mazza da baseball che colpisce una palla o, ancora, quella che un muro imprime a una macchina che vi si schianta contro.
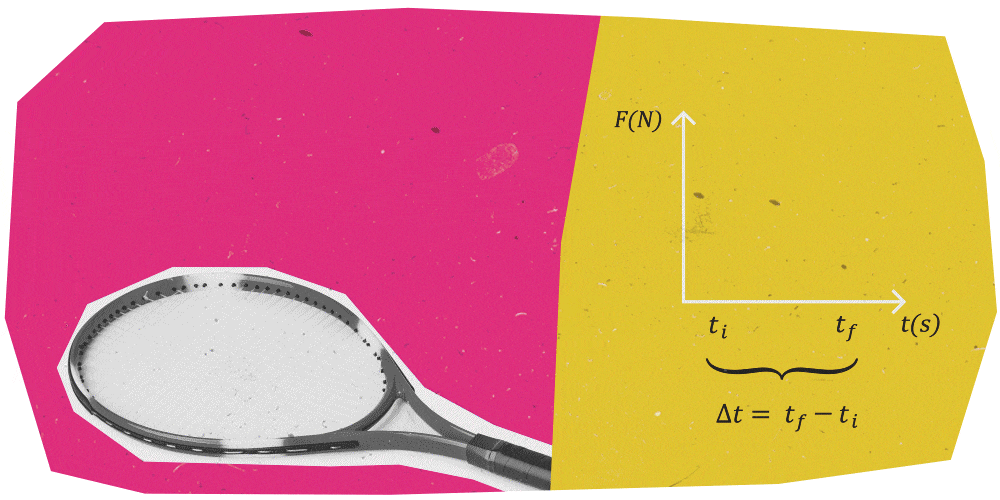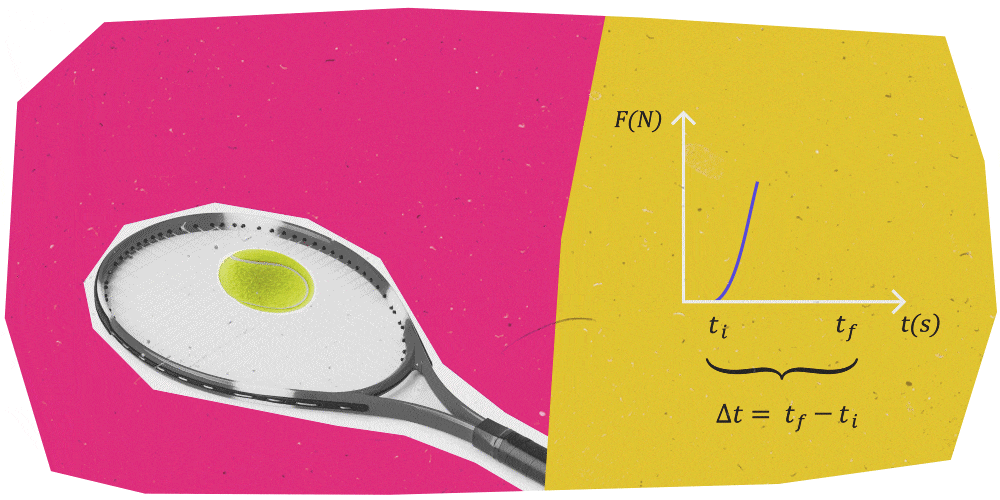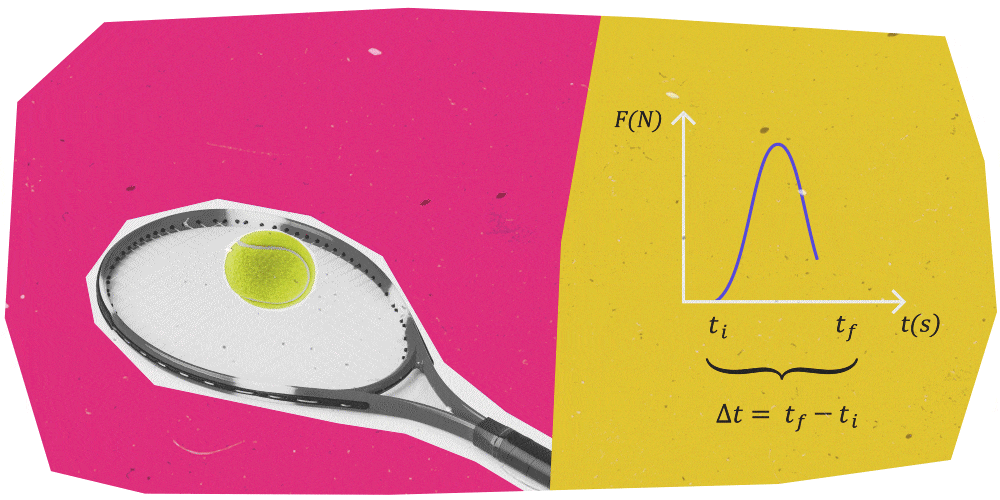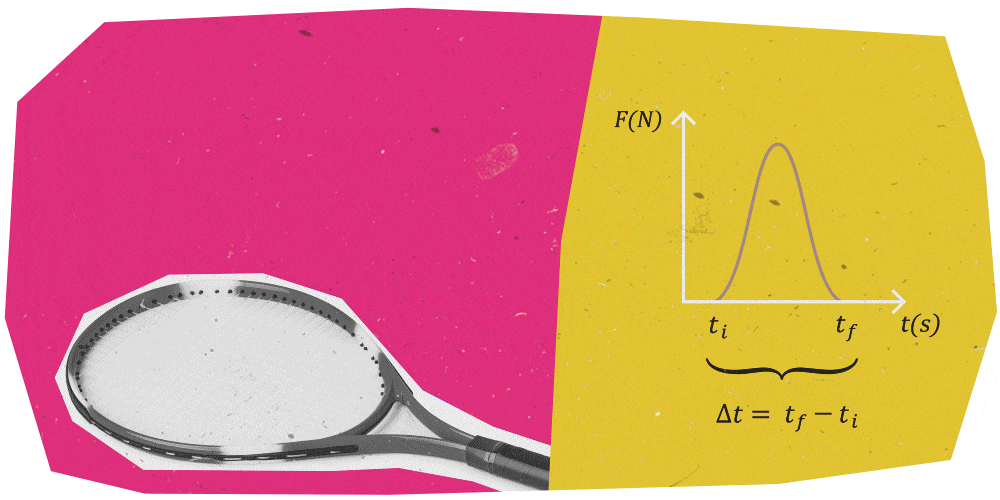
Pensa a un giocatore di tennis che colpisce una pallina con una racchetta.
Se l'impatto inizia al tempo \(t_{f}\) , allora la forza in quel momento è nulla.
Man mano che la pallina da tennis impatta contro la racchetta, la forza aumenta perché aumenta anche la superficie che la pallina espone alla racchetta. Quando la velocità della pallina diventa nulla, la forza che la racchetta esercita su di essa raggiunge il suo valore massimo.
Da quel momento in poi la pallina inverte il suo moto e si stacca progressivamente dalla racchetta facendo diminuire la forza esercitata.
La diminuzione termina al tempo \(t_{f}\) quando la forza torna ad essere nulla.
Questo tipo di forze sono dette forze impulsive. II nome «forze impulsive» è dovuto ad una grandezza fisica che permette di darne una descrizione in termini più immediati: il vettore impulso \(\vec{I}\).
Che cos’è l’impulso di una forza?
L'impulso ci dà un'informazione su come una forza agisce in un certo intervallo di tempo. Per capire come è definita questa grandezza fisica, consideriamo prima il caso di una forza \(\vec{F}\) costante che agisce in un intervallo di tempo \(\Delta t\).
L'impulso di una forza costante è definito come:

Dunque il vettore impulso ha la stessa direzione e lo stesso verso della forza \(\vec{F}\) e la sua unità di misura nel SI è \(N \cdot \mathrm{s}\), o equivalentemente \(\mathrm{kg} \cdot m / s\), cioè la stessa unità di misura della quantità di moto.
Possiamo dare un'interpretazione geometrica del suo modulo.
Infatti, se rappresentiamo il modulo della forza \(\vec{F}\) su un grafico forza-tempo, osserviamo che il prodotto \(F \Delta t=F\left(t_{f}-t_{i}\right)\) non è altro che l'area di un rettangolo che ha per base l'intervallo di tempo e per altezza il valore di \(F\), cioè del rettangolo che il grafico di \(F\) forma con l'asse delle ascisse e le rette verticali passanti per \(t_{i}\) e \(t_{f}\).
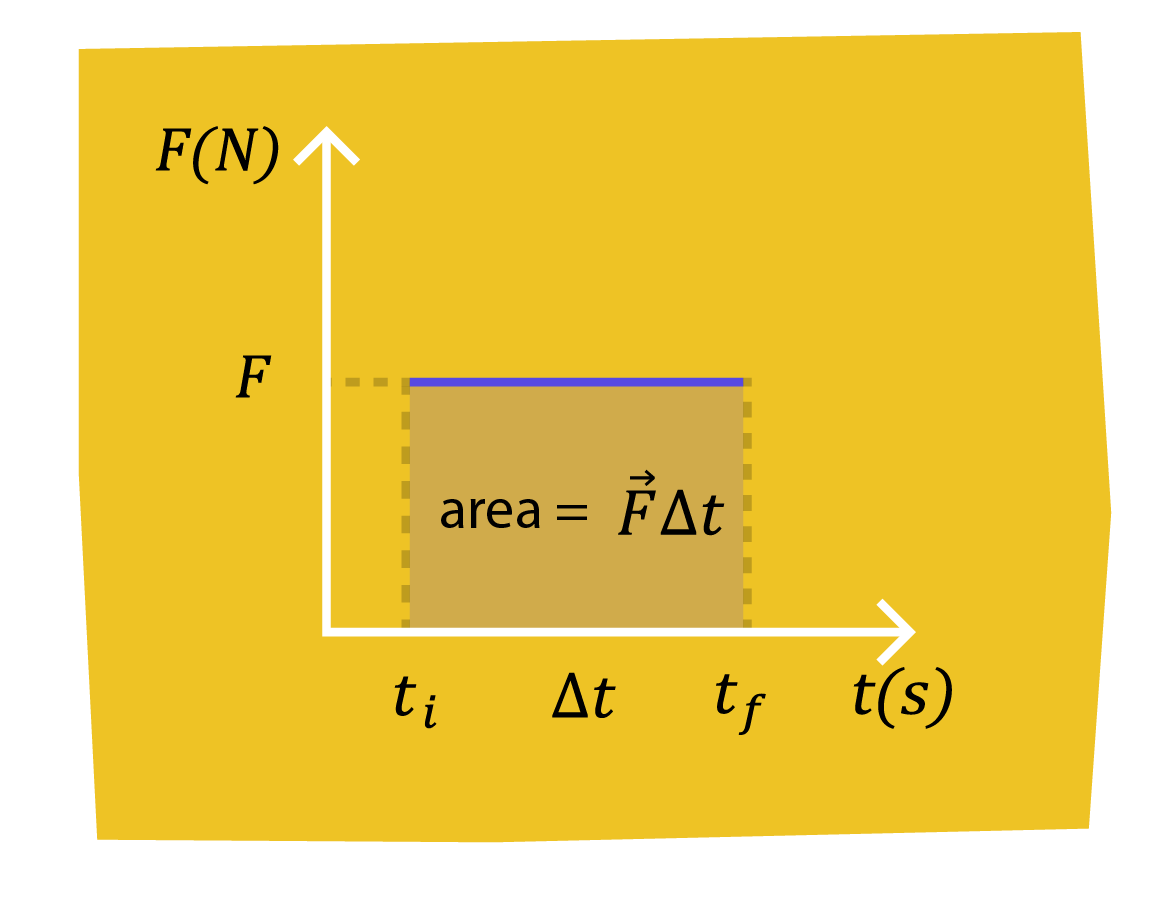
Consideriamo adesso il caso generale di una forza \(\vec{F}\) non costante.
La definizione di impulso data nel caso di \(\vec{F}\) costante non ha senso in questo contesto perché \(\vec{I}\) è un vettore, mentre \(\vec{F}\) varia nel tempo quindi a ciascun istante di tempo corrisponderebbe un diverso vettore.
Quello che continua invece a valere è l'interpretazione geometrica del modulo dell'impulso, che è nuovamente uguale all'area sottesa dal grafico di \(F\) nell'intervallo da \(t_{i}\) a \(t_{f}\).
Pur non avendo gli strumenti matematici per calcolare direttamente l'area a cui siamo interessati, possiamo sfruttare un importante teorema del calcolo integrale che ci assicura che la nostra figura è equivalente a un rettangolo che ha per base l'intervallo da \(t_{i}\) a \(t_{f}\) e per altezza un preciso valore \(F_{m}\) che dipende dal grafico di \(F\) e dall'intervallo \(\Delta t=t_{f}-t_{i}\). Tale valore indica il modulo della forza media \(\vec{F}_{m}\) che è stata esercitata nell'intervallo \(\Delta t\).
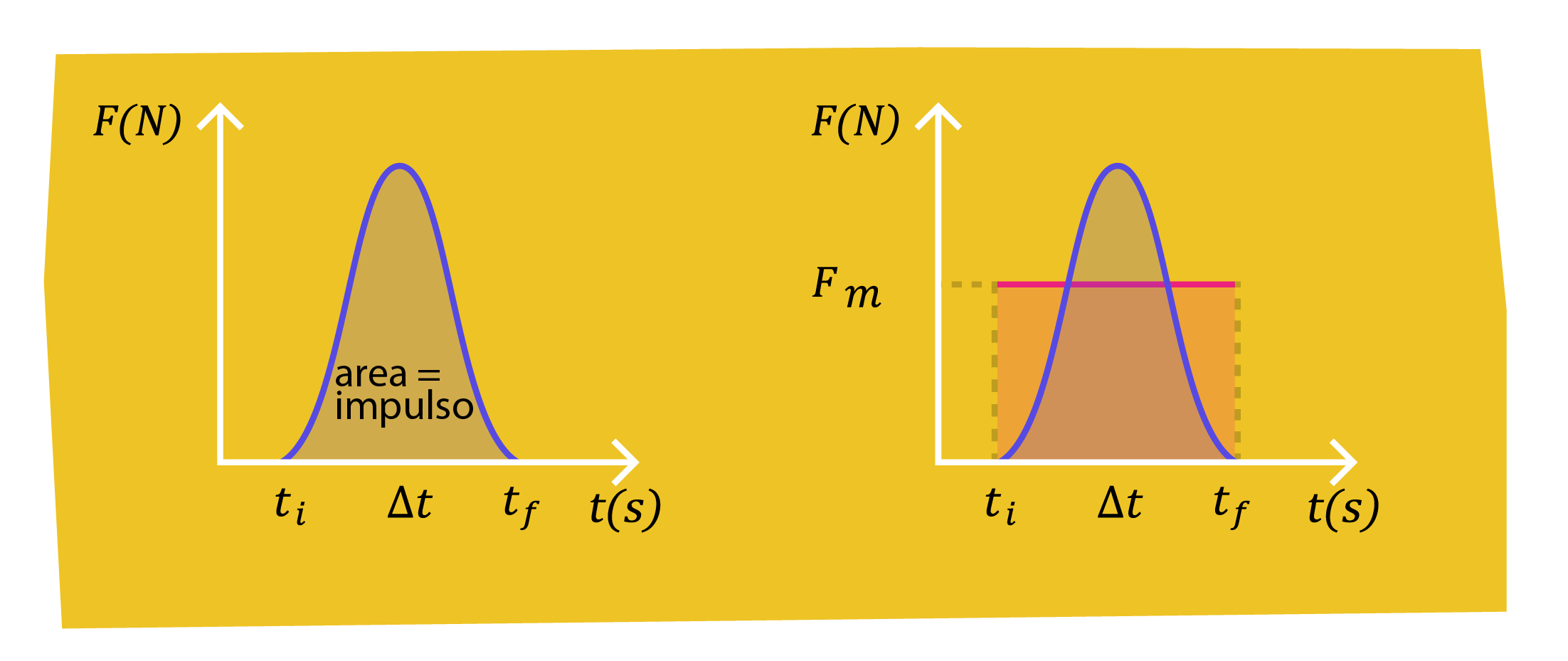
Poiché l’area del rettangolo è data dal prodotto di base per altezza, avremo che, in modulo, \(I=F_{m} \Delta t\) .
Possiamo quindi dare una definizione generale dell’impulso di una forza:
L'impulso di una forza \(\vec{F}\) che agisce per un intervallo di tempo \(\Delta t\) è il prodotto della forza media \(\vec{F}_{m}\) che agisce nell'intervallo \(\Delta t\) per l'intervallo \(\Delta t\) stesso:
